从线性拟合到深度神经网络
前几年人工智能还没火起来的时候,为了打比赛学了一点,结果当时也没找到什么好的门路,学的一知半解,模型倒是会用了,但对原理还是一知半解。最近因为某些原因,决定重新捡起来精学一下,或许是因为人工智能成功火了起来,优质课程越来越多,也越来越好寻找。找了半天之后,决定看李宏毅老师的机器学习课;第一堂花了两个小时从线性拟合讲到深度学习,直接给我整不会了。好痒啊,要长脑子了.jpg
虽然一直以来对深度学习的各概念有所了解,但是毕竟古话说得好,“知其所以然”。我比较确信,自己正处在一种知道这个东西,并且大概知道怎么用,但并不了解原理的状态之中。换句话说,扔给我一个模型,我能让它跑起来,但如何让它结果更好、跑的更快,就超出能力范围了。这时候恰好遇到了李老师的机器学习课,以一种开了全图挂的美妙方式,在讲述神经网络数学原理的同时,还介绍了拟合函数是如何一步步从单调的线性拟合发展成灵活的,个中思路或许并不是其真实的发展路程,然而足够合理,让我能够理解并记住神经网络为什么会发展为如此形态,故在此记录,防止再次忘记。
1. 最基础的模型:线性拟合
首先从最广义的角度来看,数学建模,就是一类寻找特定函数
2. 更多的信息:线性组合的线性叠加
通过简单地更换函数的类型,比如将线性函数
俗话说得好,力大砖飞。正如人懂得越多越聪明一样,为了让数学模型更加准确,一种最为直接的方法是向模型中添加更多的自变量。这种修改使得模型中的自变量从单个
3. 更精致的拟合:激活函数
模型预测值与实际值之间的差距被称为模型偏差model bias。显然,模型偏差越小,其预测效果越好。然而,线性拟合,或者说是大部分基本函数,在广阔的定义域上,通常并不具有一个稳定的值,调整参数时会使其在整个定义域上的函数值发生明显变化,我称其为“按下葫芦起了瓢”——通过梯度下降等优化算法调整参数后,某些预测效果特别差的样本得到了提升,然而同时可能存在某些预测效果较好的样本,因为其参数被修改,反而预测效果变差了。换句话说,当模型效果无论怎么训练都无法提升时,其最小偏差即可视为模型误差。
面对基本函数“牵一发而动全身”从而产生的模型偏差问题,最直接的应对思路无疑就是寻找不具有这类特征的函数。换言之,我们可以使用定义域有限的函数进行更加细致的准确度优化。考虑到定义域有限制,而表达方式最为通用的函数,无疑就是分段函数了:取两个点,将函数分为三段,左右侧均为常数值,中间为单调变化的曲线,从左端点值过渡到右端点值:
这样就得到了一个相对完美的函数:在给定的定义域内为变量,在给定定义域之外为常量,满足了对模型更加精细调控的要求。在此将这种函数称为斜坡形函数。
通过将两个斜坡形函数叠加,还能实现更加优雅的函数值调控。构造具有相同形状、但相位不同的两个斜坡形分段函数:
将两式相减,得到
,直接将
(ps:md个烂typecho,写个css乱用通配符,害得我公式都变形了,调了半天才搞好)
此时的
那么如何构建这种形式的函数呢?答案是对使用惊人的注意力不难发现,可以将斜坡形函数拆分为两个更加简单的折线形函数:
是不是眼熟起来了?是的,芝士ReLU函数(Rectified Linear Unit,带修正的线性单元)。由于在计算机中可以较为轻松地依据数据符号进行条件运算,因而ReLU函数不仅具有良好的数学性能,在实际的模型演算过程中也有得到广泛应用。
根据我个人理解,activation function。估计激活这个名字来源于神经网络,意味着神经元对任意外部条件做出的响应,被映射(编码)为一种固定的表达方式。
既然是“统称”,那么自然还有其他的激活函数。不知道是不是出于梯度计算的考虑,其余常见的激活函数都是在定义域上连续可导的,如Sigmoid和tanh:
以Sigmoid为例,引入了激活函数的线性回归模型现在演化成了这个样子:
4. “我全都要”:神经网络
(这是书呆子 这是手指.jpg)诶!如果我们结合第二步跟第三步的思路,既引入多个自变量增加已知信息,又引入激活函数降低模型偏差,岂不美哉?
没错,这就是神经网络。按上述思路改进后,得到如下形式的数学模型:
可以看到,模型由多个包含激活函数的子模型(“神经元”)构成,每个神经元将所有自变量作为输入,经过激活函数计算后进行累加汇总,得到最终结果。借用李老师公开课上的图来看,现在的数学模型长这个样子:
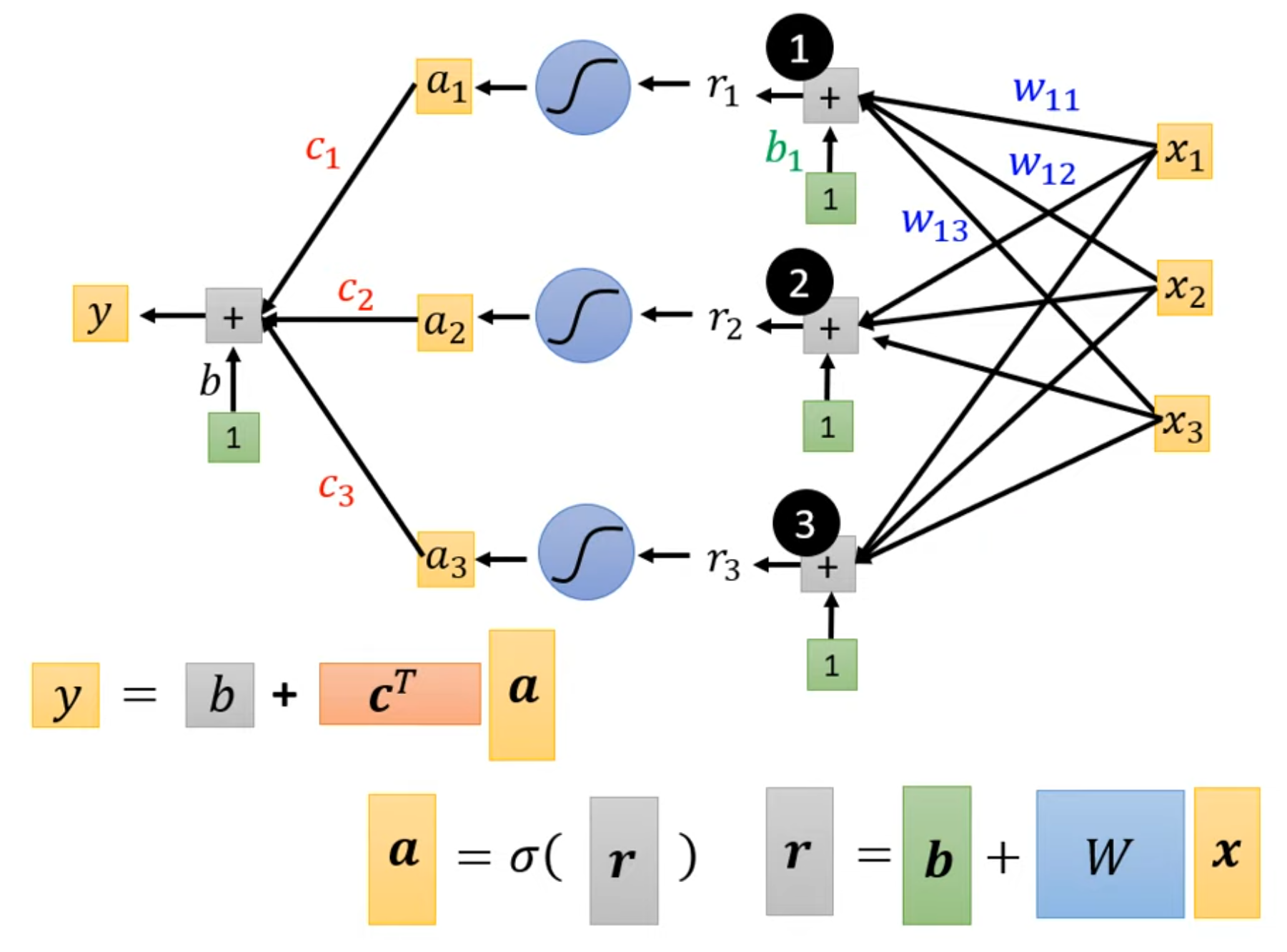
可以看到,相比于传统的单函数模型,这种模型可近似看作多个子模型独自处理输入,然后汇总成输出,更加贴近人类,或者是神经元处理事件的模型。或许这就是其被称作神经网络的原因吧。从李老师的实验可以看出,使用(单层)神经网络相对于线性回归模型,其准确度有所提升——但显然还不够。
5. “大力出奇迹”:多层神经网络
上述数学模型的发展过程无疑验证了一个道理:大力出奇迹。随着入参和数学模型的规模和复杂度提升,其模型准确度也在或多或少、但是稳定地提升。那么问题来了:如何在神经网络的基础上,进一步提升数学模型的准确度?
扩大输入规模不失为一种有效的方法。然而,在数据集规模固定,或是出于性能要求限制了输入规模的情况下,就需要依靠更加优质的模型结构来提升其精准度了。在今天——AI进入人们——或者至少我的视野近八年的时间内,不论是其神经元结构,还是激活函数的构造,都大同小异,但是模型的性能却得到了质的飞跃。究竟是什么改变了神经网络?
答案是神经元间的拓扑结构。在第4节的数学模型中,“神经元”之间仅仅是并列关系,都只是按照自己的喜好对输入数据赋不同的权重,然后给出输出值;神经元之间没有任何“交流”。
从第4节的图中不难看出,神经网络具有“多输入、单输出”的特征。什么概念具有类似的结构呢?我想,答案应该是逻辑门。在数字逻辑电路的世界里,多个二元值进入逻辑门后,根据给定的真值表,将会得出一个固定的输出值;而这个输出值作为输入值在逻辑门上的映射,将带着输入值的特征,作为输入值进入下一个逻辑门;通过这种方法,计算机科学家们使用逻辑门构建出了当今千姿百态的处理器世界。相似地,如果提升现有的单层神经网络的维度,即取多个神经网络,并计算它们的输出值;然后,再取一个神经网络,将上一级每个神经网络的输出作为输入值,得到一个新的输出值,像下图所示,不就在神经网络的基础上,实现了模型结构的又一次进化吗?
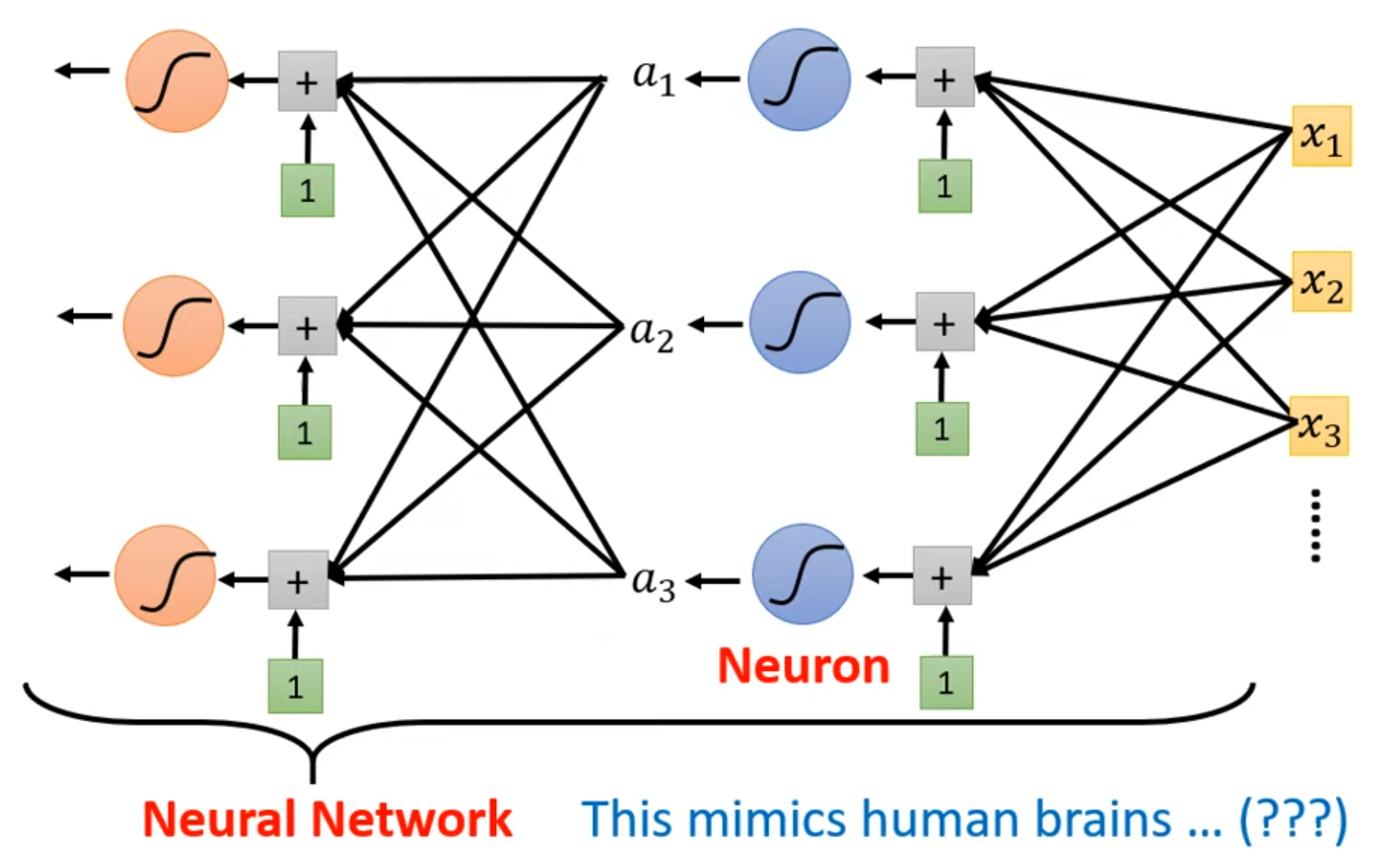
反向传播back propagation为多层神经网络的实现提供了可能。但是效果好不好呢?尝试一下总是没有损失的。这一试可不得了:DNN,CNN,RNN,GAN,LSTM,BERT,Transformer,GPT... 一个个熟悉的名词如井喷式涌出。是的,仅仅是通过搭积木似的将神经网络进行二维组合,学术界就能拿着玩好几年,直到现在大火的各种AI聊天、按要求生成图片/音频/视频等等,无一不是建立在深度神经网络的基石之上。
那么,引用The Fabric of Cosmos里一段非常经典的话:
How could this be?
Does it bother us? Absolutely.
是的,为什么深度神经网络能够做到传统模型做不到的事情,它到底能做到哪些事情,甚至每一个“神经元”动作的含义,对我们而言都是需要了解的、甚至是未知的。那我们要做的,就是走进迷雾,掀开深度神经网络神秘的面纱。