洛谷 P5461 题记:二进制找规律
看了题目之后,第一反应是有点像分形,对着样例画了一下,感觉和Sierpiński三角形很像。然后就觉得,虽然模拟是肯定能够完成任务的,但是能使用简单的数学规律表达的图形,肯定就存在简单的数学公式将其绘制出来,想了一阵子发现没想出来,无фак说,题解启动!
事实证明,方法是存在的,关键就在二进制。仔细观察题目中给出的样例数据,并不存在什么对称性质的规律,仔细核实后,发现图形和分形的Sierpiński三角形也是不完全一致的,但是可以发现的是,右半个正方形的01分布规律似乎和2的倍数存在某些不可描述的问题——实际上这就意味着,可能可以通过二进制解决这个问题。而这个时候,就要拓宽思维,把所有可能的表示都写出来,不要因为未知而束手束脚(指自己)。
话不多说,上图解决一切问题:
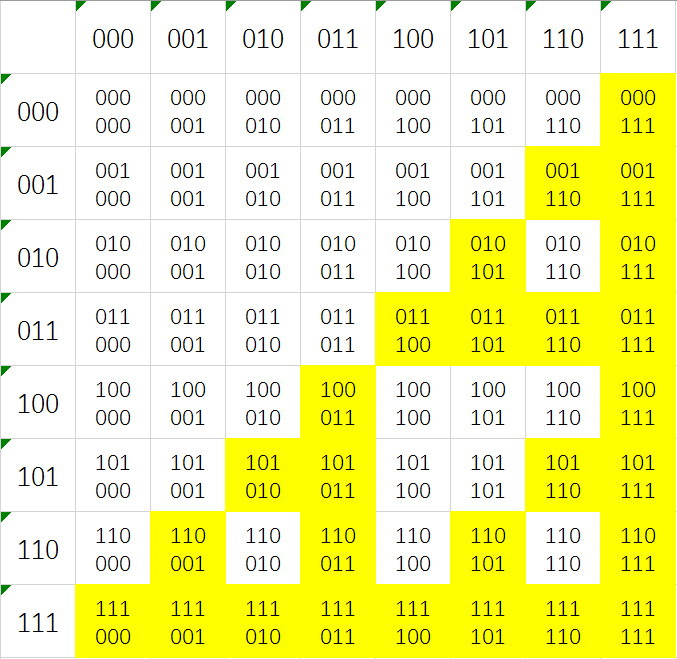
本图将这个二维点阵以0开始进行编址,给出其二进制数值,将标记为1的格子上色。仔细观察标黄的格子,不难发现,有一个很简单的特征,可以将上色和未上色的格子区分开来:所有上色的格子,对写成两行的二进制坐标进行或操作,得到“全1”,即111;未上色的格子,则得不到“全1”。为什么是三个1?这是由矩阵大小决定的,在这个样例中,矩阵大小为
那么,最后就是设计一个点阵大小的循环,对于每一个坐标进行这个与计算,并且进行判断并输出0或1。因为指数函数增长实在太快,题中只给了一个很小的数据范围(10位),其中一个取巧的办法就是使用位运算,long long类型的甚至可以装到64位,虽然这里10位就够了。