算法导论3.2-8
题目:证明klnk=Θ(n)蕴涵k=Θ(n/lnn)。
题目:证明klnk=Θ(n)蕴涵k=Θ(n/lnn)。
我怀疑你就是想开车,但是我没有证据
看某油管上的量子计算课程时,了解到了有一种东西叫做Ket Notation,即Ket标记,说的就是量子力学中常见的量子态表达方式,比如 |>外壳就是Ket标记的特征。
然后说到,Ket标记实际上是向量的一种表达方式,也就是说Ket标记可以看作一个列向量。
再之后,看到QuEST的论文里写了这么个东西:
就开始纳闷这个
然后矩阵乘法可以这么表示:
然后还没完。
根据书上写的,判断一个文法是否为LL(1)文法有三点。将其实际作用结合个人理解记录如下。
具体解释如下: 通过结合LL文法的[预测分析程序]这个实现方法的[预测分析表]可以比较直观地进行解释。LL(1)由于前看符号只有一位,可将其视作[行]为单一[非终结符],[列]为单一[终结符]的一张表格。将表格由每一固定行、列号确定的空间称作一个格子的话,则格子里放的是产生式。显然,为了由当前的分析过程和下一符号确定产生时的推导方向的话,每一个格子里只应该放最多一个产生式。当然,空下来的格子放的都是出错标记,因为当前文法不允许在该情况下进行推导。而上面的三条规则解决了如下问题:
while(1)的循环中。而显然这样的推导是失败的,因为它始终不会有结果。通过禁止左递归,避免了跳转过程中出现某些环的问题。(并非不允许环的存在,只是因为在不读入字符的情况下的环会导致无限死循环,所以只能说是禁止了“有害的”环的存在。)FOR <EVERY Non-terminal P>
FOR <EVERY Pattern α IN Production P->α1|α2|...>
FOR <EVERY Terminal e IN FIRST(α)>
prediction_table[P][e] = P->α其中P表示任意非终结符,α表示P的任意单个产生式右部,e表示α的FIRST集合里的任意元素(显然是终结符)。这么一看很容易发现,表格只有二维,而循环有三层,按照概率学的角度来说,肯定是允许在不同的α取值中,遇到同一个e的(即允许不同推导右侧的FIRST集合里有相同终结符)。从程序的角度上来说,格子里的原值要被覆盖,因为设计时是要求能够根据P和e唯一确定一个操作的;而从语法的角度上来说,格子的原值要保留,因为这代表了一条语法规则,覆盖的话会导致语法发生变化。这就产生了矛盾。所以,为了从根本上避免该情况的产生,要求在语法设计时就要避免格子出现重复赋值的问题。回到上面,不难发现解决方法之一就是要求不同的FIRST(α)里面不能有相同的e。而用专业术语来表达的话,这正是第二条规则。
FOR <EVERY Non-terminal P>
IF <EXISTS P->ε>
FOR <EVERY Terminal e IN FOLLOW(P)>
prediction_table[P][e] = P->ε相比于第二条中的工作,这里只有两层循环,因而工作内部不会出现任何问题(因为根据集合的性质,空集作为元素是不可能重复的呀)。但是该段代码与第二条中操作的是同一个预测分析表啊!因而又可能出现格子覆盖的问题。显然,解决方法又是只要两者没有相同的e就行了。这里的两者指的是FOLLOW(P)和FIRST(P)。虽然第二条的代码段中使用的是FIRST(αi),但是在认为所有元素都等价的时候(即不需要再区分每个e对应的α),完全可以算一下,FIRST(αi)并起来就是FIRST(P)。(甚至不用算好吧)
今天来当当自己的课代表:
P->α1|α2|...,∩(αi)=∅解决了在一个预测分析表里放多个非空产生式的冲突问题;P->ε,FIRST(P) ∩ FOLLOW(P)=∅解决了在一个预测分析表里空产生式与非空产生式的冲突问题。优先级去除文法的二义性 优先级在于确定无二义的文法时有重大作用,它可以确定在具有多个可选右侧的产生式中,到底选择哪个的顺序。显然这个顺序在产生式本身是无法定义的,所以需要通过多级的产生式来强行确立一个顺序:必须先完成这个表达式的匹配,才能进行下一级匹配。 由于个人的逻辑水平实在有限,发现可以作为一个规律记忆的是,最先匹配的产生式右侧,在运算时的优先级是最低的(出现多个优先级相同的运算符的话,就需要规定推导方式了,比如最左?)。也就是说,需要最先计算的表达式,是需要最后匹配的。至于为什么是这样。。暂时不知道
B ::= 1B0 | A。实际上A就是B中对称中心为空的特殊情况。之前被老师坑了,以为产生式右侧不能放ε,所以就对右侧有了奇怪的理解,比如A ::= 0A1 | 01。。。在做计算机组成题目的时候,遇到的神奇的这么一题:
假设某计算机按字编址,Cache 有 4 个行,Cache 和主存之间交换的块为 1 个字。若 Cache 的内容初始为空,采用 2 路组相联映射方式和 LRU 替换算法。当访问的主存地址依次为 0,4,8,2,0,6,8,6,4,8 时,命中 Cache 的次数是?
当时就有点纳闷:访问的主存地址都是偶数,若是最基本的组相联的映射关系的话,岂不是只有一半的缓存是有效的? 按照这种方法计算,最终是只有一次缓存命中的。
但是看着总感觉隐隐不对劲,再理论化的题目,也不应该出反实际情况的例子啊,哪有这种暴殄天物的操作。 再去翻翻书,书上也只对于Intel Pentium处理器内的2路组相联缓存做了一个让人捉摸不透的简要解释:
因为在两路组相联cache中,一个主存块只能调入cache的一个特定组的两块中的一块,因此只需设置一个标志位,当两块中的一块(假设为A块)被命中时,标志位置1,而另一块(假设为B块)被命中时,标志位清0。当需要替换是,只需检查此标志位的状态即可:为0替换A块,为1替换B块。Pentium CPU内的数据cache采用的是一个两路组相联结构,使用的就是这种简化的LRU替换算法。
(若是至此,或许可能存在的读者已经领悟其中的意思的话,可直接跳至文尾)
后来在网上找也没看到说有什么官方权威的解释,不过在某度文库的一个ppt里找到了这样的题解: https://wenku.baidu.com/view/e1c69c0cf78a6529647d5340.html 为了防止原链接抽抽,贴张截图吧
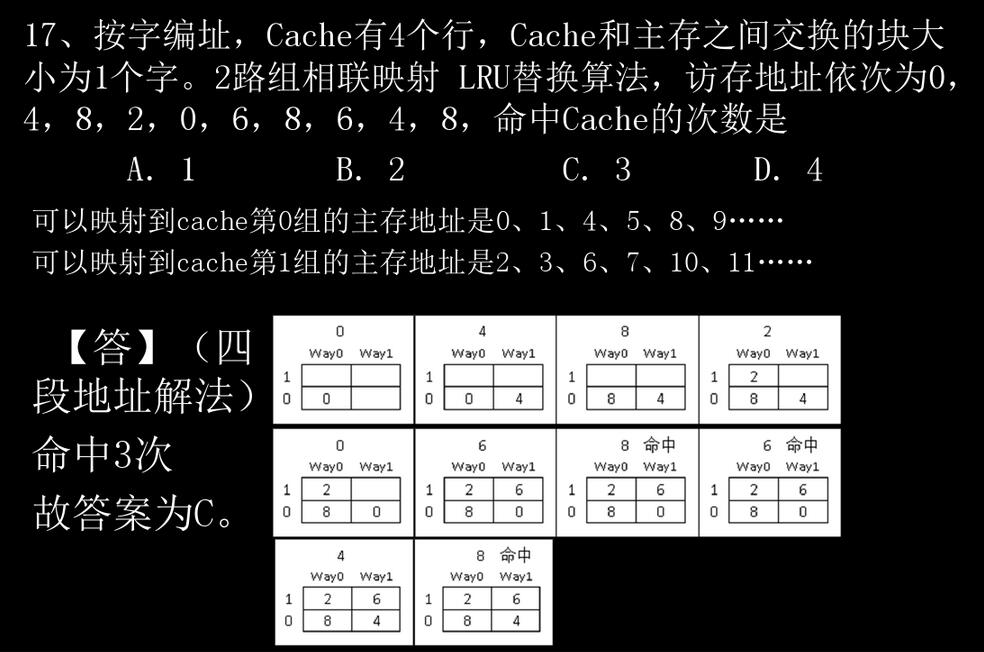
也就是说,根据这个题解在对存储单元在缓存中的映射中,采取了连续两个分为一组的规则的操作,可以大胆猜测:所谓的2路组相联操作,就是在缓存分组的时候每两个缓存单元一组,且在做映射的时候将连续的两个主存单元映射至同一组缓存分组。通过这个猜测,我们可以解释在该题解中,为什么4个缓存单元要画成2x2的形式,以及为什么分组是两个连续主存单元分至同一缓存块。
此时回过头去看上面的书本引用,会发现似乎清楚了许多:一组中只有两个缓存块,当有新数据进入时,替换的只能不是A块就是B块,因而只要根据LRU算法,哪个最近被使用的“得分”低,就会被替换出去,因而只需要一位二进制就可以表示LRU算法中的标志位。再说通俗一点,对于这个缓存块,我更愿意把它叫做“块中块”,因为首先主存在分组映射的时候,就已经需要按照一定的数学规律进行归类,而这个“2路”决定了其中归类时的连续存储单元数为2,而不是默认时的1。
据此,作出如下抽象公式式的结论: 假设有N个缓存单元可以分解为两个正整数m, n的乘积,定义n路组相联的映射规则如下: 将主存单元和N个缓存单元均按照每n个一组划分(即有m个缓存单元组),将所有(km+i)个主存单元组映射至第i个缓存单元组。 其中i为[0, m)区间内的整数,k为使得第(km+i)个主存单元组存在的自然数值。
但是,到目前为止,尚未见过2路以上的组相联缓存映射。 假设要实现的话,标记为可做如下设计: 1) 一组内有多少个寄存器就用多少位二进制,用0和1区分不需要和需要替换的寄存器,可作为选通信号直接输给硬件电路; 2) 使用二进制地址来表示需要替换的寄存单元编号,用译码器传递选通信号。
没错,回去点个题,这篇文章大部分基于个人分析,目前尚未找到权威书籍或资料证明其正确性。可能是因为太懒还没找到
============================================== 后续更新
回去翻书后,发现书上没有对n路组相联进行详细的叙述。实际上,这个n路为了方便寻址和提高硬件利用率,通常会设置为2的自然数幂(1, 2, 4, 8, ...)。在做题时,需要利用的就是组相联中的路数的含义,包括 缓存的划分 和 主存的映射规则 。根据这个规则,以及部分博客所提供的定义,能够正确地完成题目。这才是重点