计算机组成中的N路组相联

在做计算机组成题目的时候，遇到的神奇的这么一题：

假设某计算机按字编址，Cache 有 4 个行，Cache 和主存之间交换的块为 1 个字。若 Cache 的内容初始为空，采用 2 路组相联映射方式和 LRU 替换算法。当访问的主存地址依次为 0,4,8,2,0,6,8,6,4,8 时，命中 Cache 的次数是？

当时就有点纳闷：访问的主存地址都是偶数，若是最基本的组相联的映射关系的话，岂不是只有一半的缓存是有效的？ 按照这种方法计算，最终是只有一次缓存命中的。

但是看着总感觉隐隐不对劲，再理论化的题目，也不应该出反实际情况的例子啊，哪有这种暴殄天物的操作。 再去翻翻书，书上也只对于Intel Pentium处理器内的2路组相联缓存做了一个让人捉摸不透的简要解释：

因为在两路组相联cache中，一个主存块只能调入cache的一个特定组的两块中的一块，因此只需设置一个标志位，当两块中的一块（假设为A块）被命中时，标志位置1，而另一块（假设为B块）被命中时，标志位清0。当需要替换是，只需检查此标志位的状态即可：为0替换A块，为1替换B块。Pentium CPU内的数据cache采用的是一个两路组相联结构，使用的就是这种简化的LRU替换算法。

（若是至此，或许可能存在的读者已经领悟其中的意思的话，可直接跳至文尾）

后来在网上找也没看到说有什么官方权威的解释，不过在某度文库的一个ppt里找到了这样的题解： https://wenku.baidu.com/view/e1c69c0cf78a6529647d5340.html 为了防止原链接抽抽，贴张截图吧

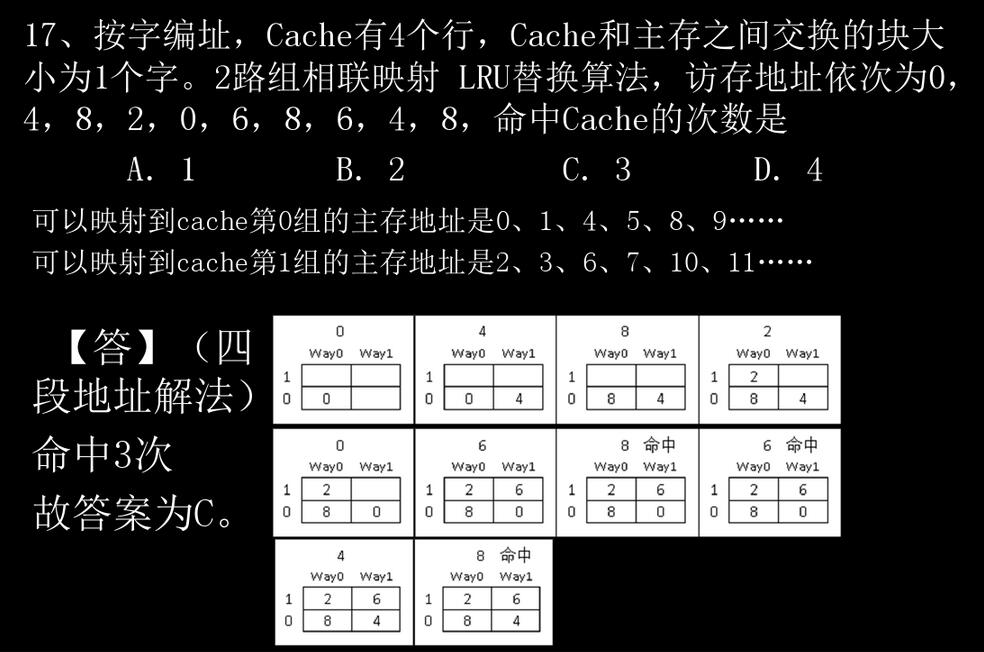
也就是说，根据这个题解在对存储单元在缓存中的映射中，采取了连续两个分为一组的规则的操作，可以大胆猜测：所谓的2路组相联操作，就是在缓存分组的时候每两个缓存单元一组，且在做映射的时候将连续的两个主存单元映射至同一组缓存分组。通过这个猜测，我们可以解释在该题解中，为什么4个缓存单元要画成2x2的形式，以及为什么分组是两个连续主存单元分至同一缓存块。

此时回过头去看上面的书本引用，会发现似乎清楚了许多：一组中只有两个缓存块，当有新数据进入时，替换的只能不是A块就是B块，因而只要根据LRU算法，哪个最近被使用的“得分”低，就会被替换出去，因而只需要一位二进制就可以表示LRU算法中的标志位。再说通俗一点，对于这个缓存块，我更愿意把它叫做“块中块”，因为首先主存在分组映射的时候，就已经需要按照一定的数学规律进行归类，而这个“2路”决定了其中归类时的连续存储单元数为2，而不是默认时的1。

据此，作出如下抽象公式式的结论： 假设有N个缓存单元可以分解为两个正整数m, n的乘积，定义n路组相联的映射规则如下： 将主存单元和N个缓存单元均按照每n个一组划分（即有m个缓存单元组），将所有(km+i)个主存单元组映射至第i个缓存单元组。 其中i为[0, m)区间内的整数，k为使得第(km+i)个主存单元组存在的自然数值。

但是，到目前为止，尚未见过2路以上的组相联缓存映射。 假设要实现的话，标记为可做如下设计： 1) 一组内有多少个寄存器就用多少位二进制，用0和1区分不需要和需要替换的寄存器，可作为选通信号直接输给硬件电路； 2) 使用二进制地址来表示需要替换的寄存单元编号，用译码器传递选通信号。

没错，回去点个题，这篇文章大部分基于个人分析，目前尚未找到权威书籍或资料证明其正确性。可能是因为太懒还没找到

============================================== 后续更新

回去翻书后，发现书上没有对n路组相联进行详细的叙述。实际上，这个n路为了方便寻址和提高硬件利用率，通常会设置为2的自然数幂（1, 2, 4, 8, ...）。在做题时，需要利用的就是组相联中的路数的含义，包括 缓存的划分 和 主存的映射规则 。根据这个规则，以及部分博客所提供的定义，能够正确地完成题目。这才是重点